Authentic Tasks Have Failed Us

There are no authentic tasks, only authentic invitations.

You’ll hear about “authentic tasks” in conference presentations, journal articles, position papers, and stray tweets about what constitutes “good teaching.” When pressed, most people define that authenticity in ways that are circular or that beg other questions.

For example, Jay McTighe and others wrote the book, Designing Authentic Performance Tasks and Projects. Here is one of their early passes at defining “authentic”:

… featuring a real challenge, problem, issue; a genuine product/performance; authentic audience; and real-world constraints …

“Real” and “genuine” and “real-world,” each beg the question, “Well what do those mean?” And it is always painful to see a word show up anywhere in its own definition.

Further illustrating the challenge here, the authors of the The Mathematics Lesson-Planning Handbook define an authentic task as “a useful tool for navigating the real world” only to contradict themselves two sentences later by writing, “This does not mean that the task must be real world.”

Authentic tasks have failed us.

We need a different approach. Task authors imagine their math tasks are like a book, something they can label with a particular genre—gothic horror, romance, authentic, etc—that the reader will experience without interference. But in the classroom, teachers mediate the student’s experience of math problems. Math problems then function like books read aloud by someone who can change the plot, rearrange chapters, and alter the ending at will.

Students need authentic invitations.

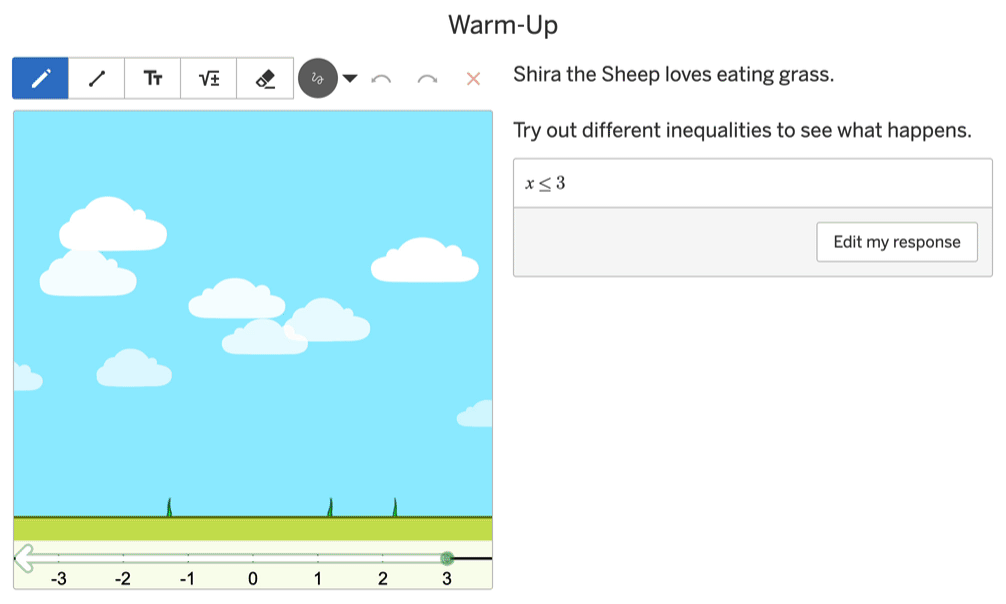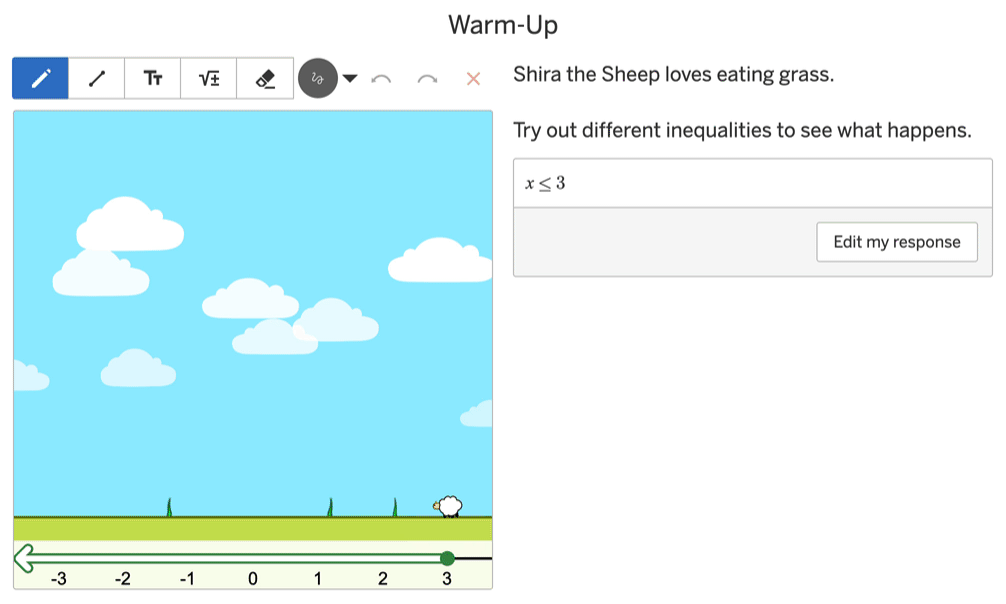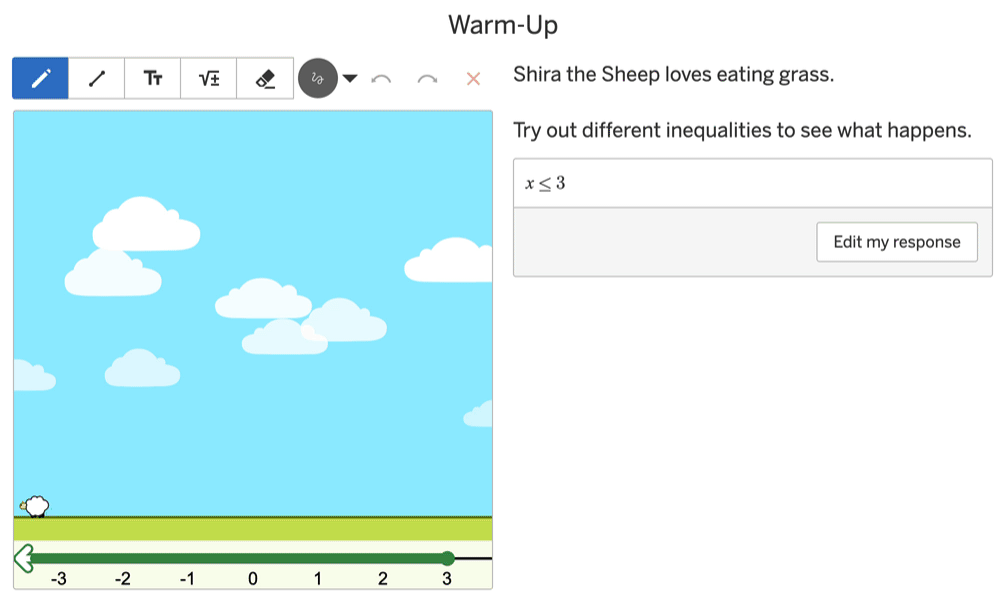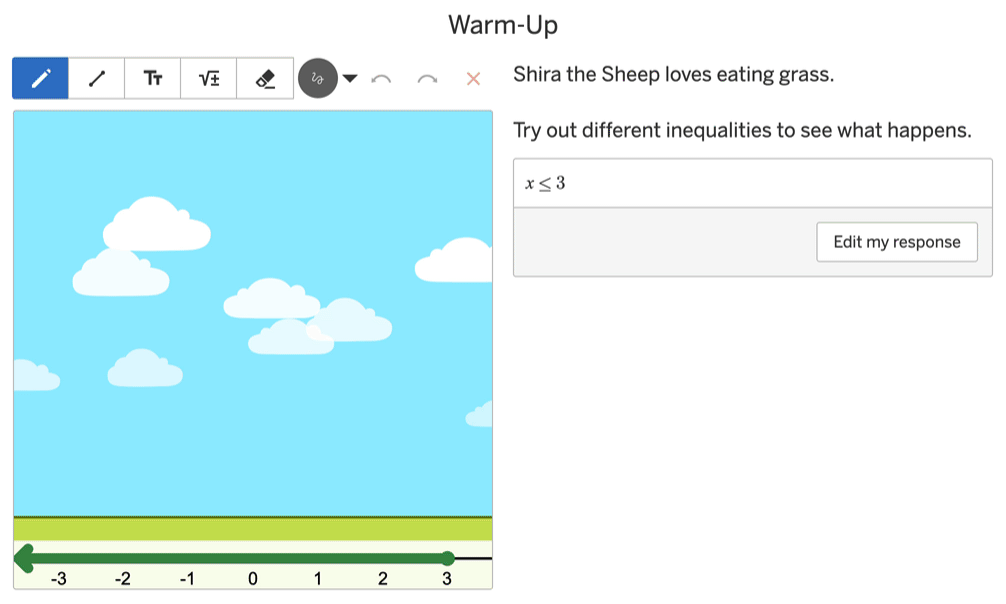
Here is a screen from our activity Shira’s Solutions where students type an inequality into a math input and watch a sheep respond. With x ≤ 3, for example, the sheep parachutes down at x = 3 and eats any grass she finds to her left.

Is this question “authentic”? Is it “real world”? I do not know and I am unburdened by any care. What I care about is—is the teacher’s invitation authentic?

Here is a 2.5-minute video of Liz Clark-Garvey teaching that screen at the start of a lesson. Liz’s generosity with her teaching practice is an ongoing gift to the rest of us and I encourage you to watch it. What do you notice?

What I invite you to notice here is that, at the start of the lesson, Liz is actively seeking divergence, rather than convergence. She asks, in essence, “was anybody surprised by what they tried out here?”

In many math classes, students come to understand that they should minimize their surprise. Every new thing you learn is supposed to follow deductively and rationally from every previous thing. In those classes, students understand they should leave their sense of surprise outside the classroom door. In Liz’s class, by contrast, students and their surprise receive an explicit welcome.

Later, Liz intentionally seeks out more divergence. One student makes Shira eat one blade of grass so Liz asks “Did anyone find an inequality that resulted in Shira being able to eat all of the grass?” Students start giving Liz inequalities with solutions that run towards the right, so she explicitly asks for solutions that run to the left. Students try to outdo one another with more and more extravagantly negative answers, from x < -3 to x < -48 to x < -100 octillion. Liz only presents delight in those responses.

You can only change your invitation.

You cannot change a student’s perception of the nature of a task. For one student, a task might be felt as “authentic” given their unique experiences and aspirations. Another student might experience that same task as inauthentic given theirs.

All you can change is you. You can change your view of students as people with gaps and deficits and liabilities to people with rich interior lives and an abundance of interesting thoughts. You can change your understanding of mathematics, aware that the more math you know, the more student ideas you’ll have prepared yourself to invite and welcome. You can change your pedagogy, developing questions that draw more ideas out of more students with less and less cost to them.

You can change the authenticity of your invitation, asking yourself:

• Am I interested in my students as objects or as subjects?

• Do I see them as means to my own ends, or as ends unto themselves?

• Out of all of the earnest thoughts my students might have here, how many of them would delight me?

Eventually, your interest in inviting more students will direct you towards different kinds of math tasks. You won’t care whether or not the arbiters of real-ness or authenticity define them as “real” or “authentic.” You’ll only wonder, “Will this help me extend a more authentic invitation to more students?”

Related: John Mason on “rich” tasks: “It is the ways of thinking that are rich, not the task itself.”