If Math Is The Aspirin, Then How Do You Create The Headache?

A generative metaphor for teaching math.

I could tell you where similar figures are used in the world. I could tell you about lots of professionals who use similar figures in their careers. I could sit several of them down for on-camera interviews discussing the contribution similar figures have made to their professional success. Each of those professionals could be living the life of a student’s dream and testify that this life was only possible through the study of similar figures, and I swear to you those testimonies would not increase a student’s heart rate one bit as they solve problems like this:

A model kitchen is 12 inches wide. If it was built with a scale of 3 cm : 4 m then how wide is the real kitchen?

It was in grad school that I first encountered Guershon Harel’s “necessity principle” and his description of the five intellectual needs for mathematics that teachers can invite students to experience. That principle—a reformulation of Piaget’s ideas about disequilibrium—unlocked for me a whole world of engaging mathematical experiences that were and I think still are kind of uncommon. For example, check out this introduction of point labels in geometry, an application of Harel’s “need for communication.” Uncommon and interesting!

At Desmos Classroom, we expressed that principle through digital technology, creating experiences like this one where students have two options: (1) manually complete the next 24 terms of a pattern or (2) describe it with one equation. The first option helps student experience the need for the second.

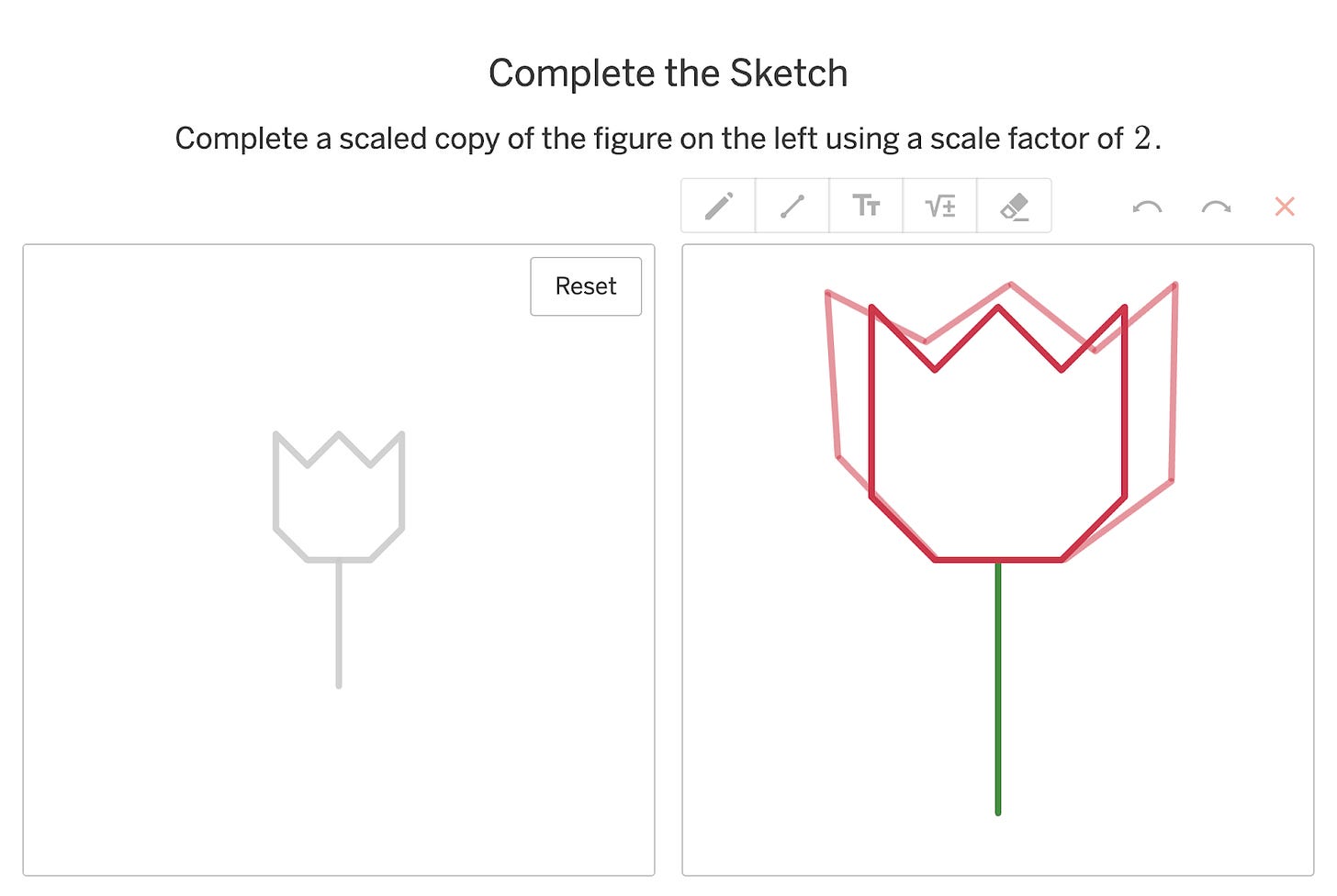
Or this experience where students encounter the need for scale drawings when they try to create one without a grid, first, and later with a grid.

Uncommon and interesting! Undergirding these experiences is the conviction that students should experience a need for new math now, rather than in some abstract promised future.

All of that is just preface for another July throwback post where I offer up a metaphor that continues to nourish my work today. Math is generally taught like it’s a vitamin. Something you’ll need for future health. Better bone density when you’re older, etc. But we can and should teach math like it’s aspirin for a headache you’re experiencing now.

---

Several months ago, I asked you, “You’re about to plan a lesson on concept [x] and you’d like students to find it interesting. What questions do you ask yourself as you plan?”

There were nearly 100 responses and they said a great deal about the theories of learning and motivation that hum beneath everything we do, whether or not we’d call them “theories,” or call them anything at all.

• “How can [x] help them to see math in the world around them?”

• “How can I connect [x] to something they already know?”

• “How can I explain [x] clearly?”

• “What has led up to [x] and where does [x] lead?”

You can throw a rock in the math edublogosphere and hit ten lessons teaching [x]. They might all be great but I’d bet against even one of them describing some larger theory about learning or mathematics or describing how the lesson enacts that theory.

Without that theory, you’re left with one (maybe) great lesson you found online. Add theory, though, and you start to notice other lessons that fit and don’t fit that theory. When great lessons don’t fit your theory about what makes lessons great, you modify your theory or construct another one. The wide world of lesson plans starts to shrink. It becomes easier to find great lessons and avoid not great ones. It becomes easier to create great ones. Your flywheel starts spinning and you miss your highway exit because you’re mentally constructing a great lesson.

Here is the most satisfying question I’ve asked about great lessons in the last year. It has led to some bonkers experiences with students and I want more.

• “If [x] is aspirin, then how do I create the headache?”

I’d like you to think of yourself for a moment not as a teacher or as an explainer or a caregiver though you are doubtlessly all of those things. Think of yourself as someone who sells aspirin. And realize that the best customer for your aspirin is someone who is in pain. Not a lot of pain. Not a migraine. Just a little.

Piaget called that pain “disequilibrium.” Neo-Piagetians call it “cognitive conflict.” Guershon Harel calls it “intellectual need.” I’m calling it a headache. I’m obviously not originating this idea but I’d like to advance it some more.

One of the worst things you can do is force people who don’t feel pain to take your aspirin. They may oblige you if you have some particular kind of authority in their lives but that aspirin will feel pointless. It’ll undermine their respect for medicine in general.

Math shouldn’t feel pointless. Math isn’t pointless. It may not have a point in job [y] or [z] but math has a point in math. We invented new math to resolve the limitations of old math. My challenge to all of us here is, before you offer students the new, more powerful math, put them in a place to experience the limitations of the older, less powerful math.

I’m going to take the summer [ten years ago, not now -DM] and work out this theory, once per week, with ten skills in math that are a poor fit for other theories of interest and motivation. As with everything I have ever done in math education, your comments, questions, and criticism will push this project farther than I could push it on my own.

The first skill I’ll look at it is factoring trinomials with integer roots, ie. turning x^2 + 7x + 10 into (x + 5)(x + 2). All real world applications of this skill are a lie. So if your theory is “math is interesting iff it’s real world,” your theory will struggle for relevance here.

Instead, ask yourself, “Why did mathematicians think this skill was worth even a little bit of our time? If the ability to factor that trinomial is aspirin for a mathematician, then how do we create the headache?”

---

I would run teacher workshops on these ideas over the next several years. I’d ask that same question and the participants and I would brainstorm answers for different mathematical ideas. We compiled them. It was a joy.