Kids' Thoughts Aren't Broken
On mistakes and misconceptions.
If you ask any secondary math teacher what incorrect idea students have about math that they'd most like to correct, the odds are very, very good they'll mention an idea Bowman Dickson memorably called The Dead Puppy Theorem:
"How do we rid students of this misconception?" math teachers often ask. "Why does this mistake persist!?"
But it's important to first reject the framing of this incorrect idea as either a misconception or a mistake. The prefix "mis" connotes something deviant or poorly formed. But this idea is, in fact, very sensibly formed by the student in response to lots of features of their environment, most notably their curriculum and instruction!
Check out how the distributive property is introduced in two different curricula. How can you blame students?
In the human mind, every idea not explicitly forbidden is implicitly allowed. We can wish the process of learning were another way, but it’s this way instead.
In both excerpts above, students see that the distributive property means you can apply a group operation to individual terms. Both definitions tell you they're talking about multiplication over addition, but neither explicitly forbids other operations.
Learners take ideas that we only meant for one part of the world and—consciously or unconsciously—try them out in other areas. They over-generalize. They ride their bikes through the restaurant drive-thru. They take scissors to the cat’s whiskers. They use a vacuum to rake leaves. This is what humans do when they learn.
Rochelle Gutierrez invites us to stop naming this process as deviant:
… students don’t have misconceptions. They have conceptions. And those conceptions make sense for them, until they encounter something that no longer works. They are only “misconceptions” when we begin with the expectation that others need to come to our way of thinking or viewing the world.
All of this is an introduction for a slide that captivated me and my Twitter mutuals the other week.
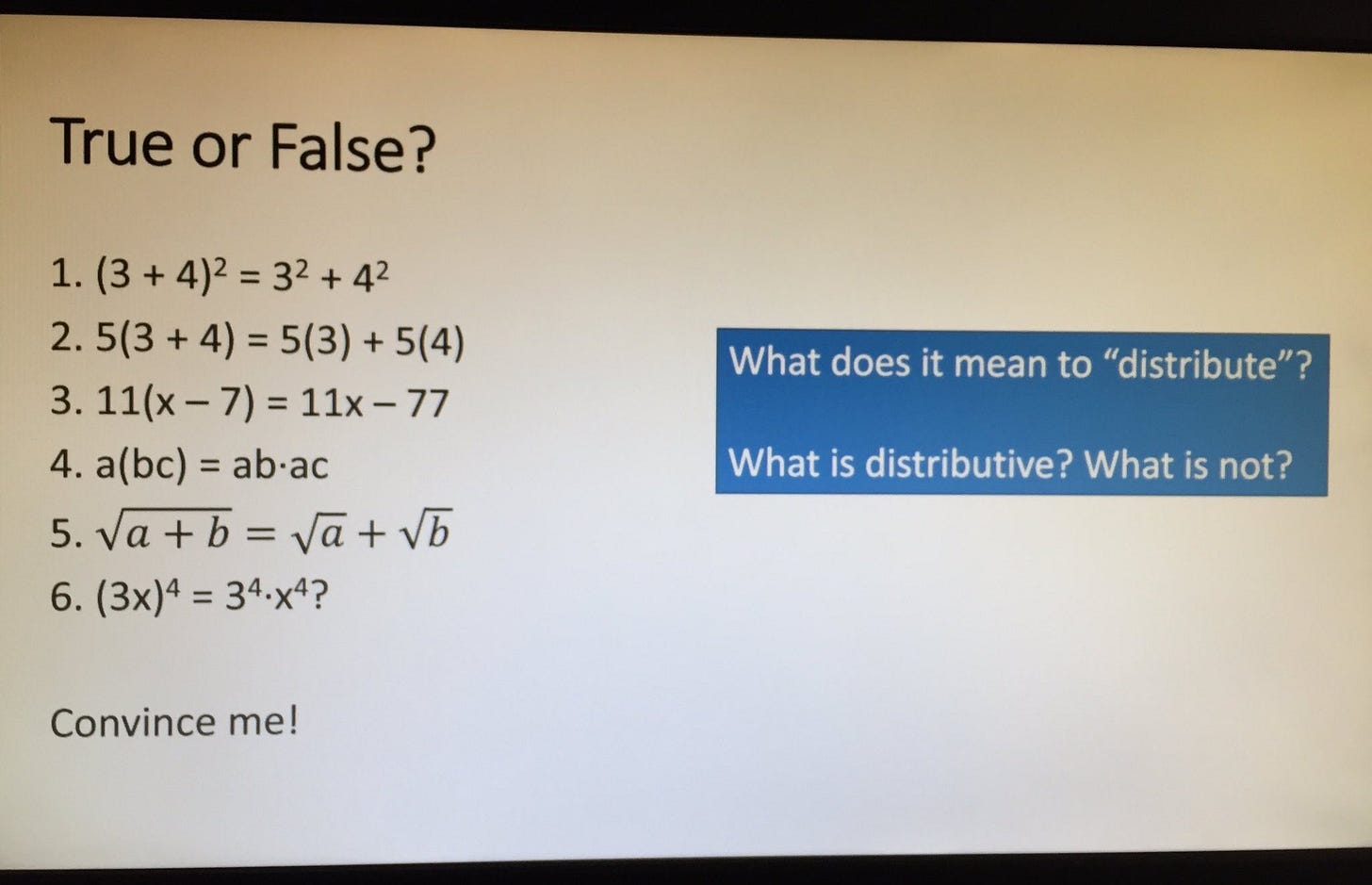
Notice how it offers learners a chance to find the edges of the distributive property through examples but also counterexamples. Over-generalization often results when students only experience positive examples. Too many negative counterexamples in sequence, however, and students might wonder, "Wait—does this idea apply anywhere?" This slide offers both opportunities.
Teachers develop people and their ideas. That's the work, and success requires us to take both ideas and people very seriously. It requires a default assumption that kids aren't broken and neither are their thoughts. Instead, both are in constant motion, constant change, and the work and pleasure of teaching for me is the chance to witness and support that change.
What Else?
Area Man Who Talks a Lot About Teaching Teaches His First Full Day in >10 Years. A few reflections from yours truly on being a substitute teacher in my local district.
The team at Desmos just released feature improvements that makes it like 5000% easier to give students feedback and share student work.
New episode of my Math Teacher Lounge show with Bethany Lockhart Johnson! We chatted with Fawn Nguyen about problem solving.
“How can/should I teach dividing fractions if not with keep, change, flip?” an early-career teacher asks on Twitter. Loads of people respond, and I’ve got to say: if you’re a pre-service math teacher educator and you aren’t preparing teachers to interact with one another in online spaces like Twitter, those math teachers are going to miss out on some fantastic in-service learning opportunities.
I’ll be expanding on the ideas in this newsletter in a free session for the Make Math Moments Virtual Summit this weekend. You’re invited!




Somewhat ironically, I am taking a class on Curriculum Design and submitted a video discussion for an assignment about 6 hours before Dan posted this article which aligns perfectly with what he said! The post is ~18 minutes, but the part relevant to Dan's article starts at time 0:53 if you are interested. https://content.screencast.com/users/ChadTLower/folders/Capture/media/f91f2cee-a65e-4b02-954e-614d68ad67ef/LWR_Recording.mp4
Excellent and highly useful article. Sometimes I think there are a lot of teachers who unconsciously take joy in seeing students draw erroneous conclusions. That gives them (the teachers) the chance to demonstrate to kids that teachers are necessary. What your article suggests is that instead of reveling in/bemoaning these sorts of student "mistakes," teachers should see them as evidence that curriculum materials and/or instruction aren't leading students to confront their assumptions. And that means that teachers should be taking the lead in constructing more thought-provoking, effective lessons and sets of problems.