Teacher Tune Up
Help me tune up my teaching.
I just taught a lesson to Grade 7 students—Balancing Moves from the Desmos Math Curriculum, a lesson on equivalence, equations, and hangers, a total blast.
If you're like me, every lesson is a mixture of success and failure, triumph and regret. I'm offering you here a short video of my teaching where I share one of those triumphs and also a regret, an area where I'd like your help. I'd like to tune it up. A Teacher Tune Up, if you will.
Have a look, please. Then come find me in the comments and help me figure out how to handle similar moments in the future.
2022 Apr 27
There’s at least a semester’s worth of knowledge in the comments here, over on YouTube, and in my inbox. This was exhilarating! And also nostalgic! I first started sharing my practice publicly in 2006 and will frequently claim in interviews that the combination of my transparency and the generosity and wisdom of this community helped me turn one year of teaching into two years of teaching growth. I was reminded of that feeling here as well. Thanks, everyone. Some highlights.
Lower the cost of participating.
Lots of people have noted that I made the class an expensive offer. Decide now, in front of your peers, if you agree or disagree with an argument you maybe don’t really understand yet if you were even fully tuned into it in the first place. Lots of people have recommended a “turn and talk” or a “pair share” protocol to let students clarify their thinking and rehearse their argument first.
Thanks to Shelly Herbert, Kristin Gray, Katie Derleth, Molly Vokey, Marilyn Burns, and many others.
Broaden the forms of participation.
Other people here have offered valuable protocols for broadening the ways students can respond to the argument beyond agree / disagree.
Johanna Langill summarizes this well and offers a possible solution:
I like to start with “raise your hand if you thought of it in the same way/also used splitting for yours” or “fist to 5 how much sense does it make to you to split the shape like that” and then like Scott maybe a quick- “talk to your partner about why/how he split the shapes, and if you can do that” or maybe “about how his way of doing that connects to your way of figuring it out”
I think you got stuck because the question more about is he right or wrong (ambiguous about is the method right or wrong vs his final answer that the hangar is unbalanced) vs what made him think that/why his method does or doesn’t work.
Janelle Schorg
Focus your question around Error Analysis and/or a Misconception so students have something to think about instead of a a yes/no question: For example: Why might someone say B is balanced and identify the error? (Half of 3 is 1.5. Didn't take into account the square on the left side)
Dave Kung
What it if were a regular move in class, after seeing a student's work, to ask students to turn and talk with a more specific prompt. As a pair, they have to agree to respond to one of three possibilities:
1. Agree - why do you agree?
2. Disagree - why do you disagree?
3. Ask a specific question.
Connor Wagner makes sure everyone can give an answer to his next question.
… one of the moves I will sometimes make is take a poll of the class, "put a thumbs up if you think we are "allowed" to split a square in half; put a thumbs down if you think we can't do this; put a thumb to the side if you are unsure."
Scott Farrand calls this the texture of a question. Love that.
One thought: Beyond asking whether they think it balances or not, you could ask something with more texture. Three options: does it balance, or is the LHS heavier, or is the RHS heavier? Then send them to talk with their partners, seeking agreement and explanation. The ceiling is a bit higher on that question and the issue of which side is heavier might offer access to some students who have lost the thread.
Maybe watch your tone, fella.
Loads of people note that I fumbled the ball straight into the ground and all the way to the earth’s core when I ask the kid, “Who told you that you could do that?” only to recognize him freak out and then to freak out myself and quickly clarify that “it’s all good it’s all good little buddy.” Believe me when I say I will go to my grave replaying that moment ha ha.

Video source #1 is an iPad on a Swivl. (That’s the far camera.)
Video source #2 is recorded from the webcam on my laptop. I use Screenflow here and a Logitech Brio webcam.
Video source #3 is a screen recording which is also handled by Screenflow.
Then I edited those three clips down to the segment of interest, cutting between them when it felt useful. I exported that as a video file.
Then for my commentary I used a program called Ecamm Live and a little image frame created by designer Kate Lam here at Desmos. Then I’m just yakking and scrubbing the video around in QuickTime Player.
Export that over to Youtube.

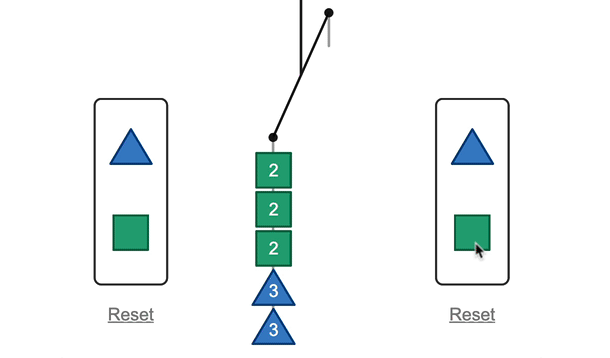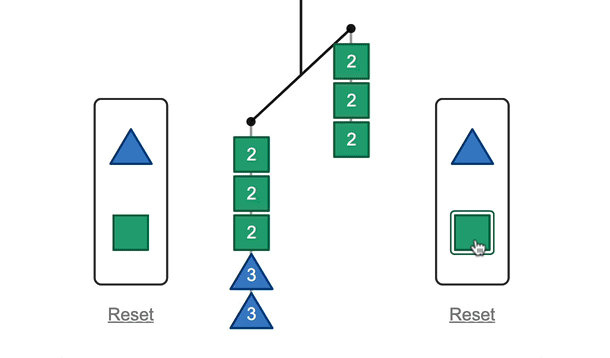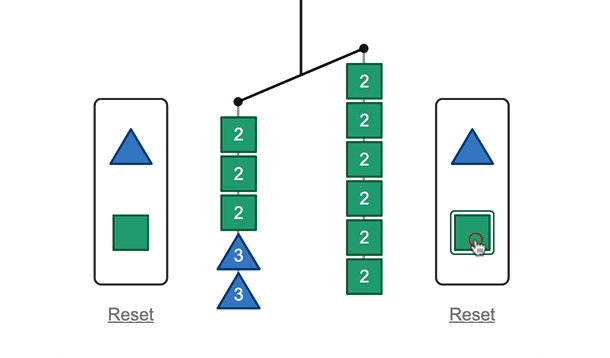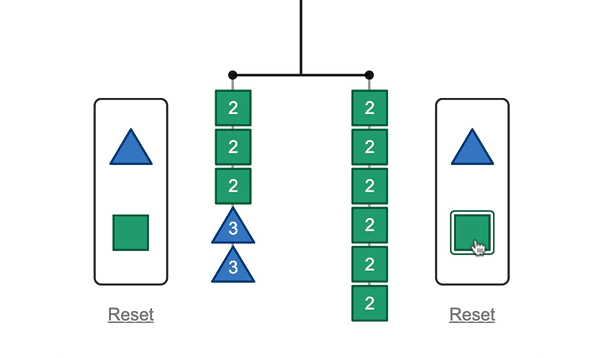
First, thanks so much for sharing the video. The vulnerability that you express matches what I feel often in the classroom when I have to make decisions in the moment, especially when a student offers an idea and I want to acknowledge the student’s participation and thinking, support the student’s agency, but the idea isn’t correct. It happened to me recently in a second-grade class and I’m still smarting a bit about how I handled it.
When the boy said that each circle was equal to 1 ½ squares, it was a Huh? moment for me. After that, you asked, “Anyone have a comment about that, agree, disagree?” That’s when I stopped the video and took the time to make my own drawing and check it out. I’m not familiar with this lesson, so maybe you quickly saw that it made sense, but I had to make sense of it for myself. And I suspect that it wasn’t something that was obvious or clear to other students.
I think it might have been helpful, after asking the others if they agreed or disagreed, to give them time to talk about it in their groups. Maybe present it as a conjecture:
S thinks that each of the circles equals 1 ½ squares. Talk in your groups about whether you agree or disagree, and why.
By moving on quickly to his conclusion, “So your answer is that it won’t balance,” I’m concerned that some students were left in the dark. During many of my college math classes as an undergraduate, many times I was left in the dark and had to find/crawl my way back after class. One of the commitments I made early on as a math teacher was to try and not leave students behind. It’s hard to live up to that commitment as a teacher, I’ve learned. Giving students time to think takes time, and the pressure of classroom teaching looms. (Henry Picciotto gave an Ignite talk about the tyranny of time in the classroom. https://www.youtube.com/watch?v=QoX6lnqzXUs
A quote from one of my educational heroes: "But putting ideas in relation to each other isn't a simple job. It's confusing and this confusion does take time. All of us need time for our confusion if we are to build the breadth and depth that give significance to our knowledge." -- Eleanor Duckworth, The Having of Wonderful Ideas and Other Essays on Teaching and Learning.
Once students see his idea, the next math challenge is for them to use that information to decide that B won’t balance. That, too, won’t be obvious to all and, again, students may need time. I think it would be time well spent.
This stuff is so hard in the moment, but the chance to reflect together like this is so great! I wonder if instead of you being first to respond, a quick turn and talk about how the shared strategy was the same or different than their own would get that nice classroom buzz going? Then bring them back together and ask: 1) did anyone (or their partner) think about it similarly and/or 2) if there were any clarifying questions for the student at the board. Really appreciate the zooming into small, specific places in the lesson with a focused question! Thanks!