Jalah Bryant Teaches the 95%
Lots of kids check out of math because they think they have to think like somebody else. Watch Jalah Bryant check them back in.
There are just two weeks left in our July program where every week we look at what it takes to teach the 95% of kids that edtech writes off. In this installment, you’ll watch Jalah Bryant, an Oregon math teacher, helping students learn to solve for x in this equation.
If you remember learning to solve for x in school, you likely remember the sense that at every moment there was one and exactly one right move.
If you loved that feeling, if it thrilled you to precisely execute a series of optimized steps a) I call you “family” b) our numbers are probably not much more than 5% of all students.
In this 66-second clip, you’ll watch Bryant do something special. You’ll see her help the other 95% of students understand that math isn’t some narrow, decaying bridge swinging hundreds of feet above a gorge, that math can sustain their intellectual weight.
What is Jalah Bryant up to here?
Teacher (Bryant)
Somehow I have to get my Xs down to one side. That's what I did.
But I feel like I'm making little Ms Bryants and I don't wanna do that.
Some people added seven first, you gotta take a risk and do one thing to get closer to the answer.
Student
I'm gonna try four.
Teacher
Or maybe, yeah maybe Camille you take care of that four
Katie, maybe you add seven on both sides.
Allison, maybe you try adding two to both sides.
Maybe you try adding 6x to both sides.
That would be crazy cuz then you all have different ways.
Conversation starters:
If the typical way students experience this math is something like “solve these ten equations exactly the way I showed you” how is this way different?
Math is often seen as an isolated discipline. Something people do by themselves. In what ways do Bryant and this activity send a different message about math?
Featured Comments
Great analysis last week on Amanda Ruch’s teaching.
She effectively draws students in by asking them to share experiences or traditions from their families as well as their opinions about what they will need to think about when making a quilt, such that there is something for everyone to ponder and share. I am curious about what happened later: what approaches did she use to support persistence in modeling with systems of inequalities?
Odds & Ends
¶ The government of Victoria, Australia has released an analysis of their $1.2 billion statewide tutoring initiative and, wow, you really do not love to see the finding, “we found that students who received tutoring learnt less than those who did not receive tutoring.” One of their recommendations is particularly interesting to me and particularly relevant for every kind of tutor right now—virtual or human:
[This tutoring intervention] is an additional and particular type of teaching that requires expertise in all elements, from selecting students and designing a tutoring model, to monitoring students' learning growth and integrating that learning with the general classroom.
/via Michael Goldstein
¶ In Hechinger, Chris Berdik asks, “What aspects of teaching should remain human?” which is notable for pulling in quotes from a wide gamut: teachers, industry types, and professors, etc. Key analysis from Berdik:
What is not clear is whether student writers will put in care and effort — rather than offloading the task to a bot — if AI becomes the primary audience for their work.



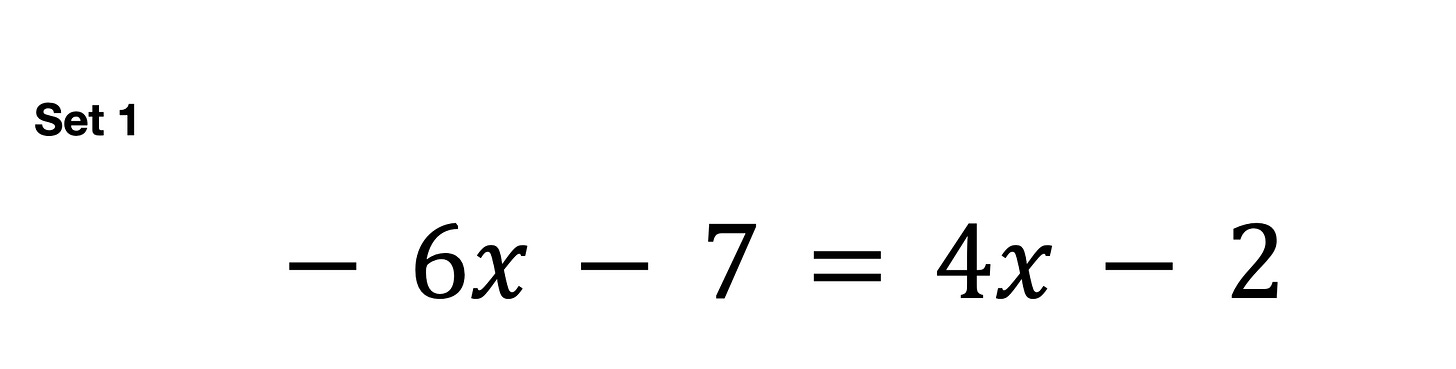
That’s an awesome clip, I’m totally stealing it when I get to work this fall (more like a week and a half). I love the idea of rotating the paper around and having students pick up where the last one left off. What a way to demonstrate that:
1. There are multiple ways to solve a problem.
2. There is valuable information to be learned from your classmates.
3. Collaborating in a group is a good thing.
4. We value the process and the product at the same time!
Too often I fall into only caring about the product, than the process.
Thanks for sharing!!
There is nothing isolated about each person in a group trying something different and then coming back to talk about the outcome. Each student has an opportunity to engage in authentic work and see the value in working toward precision. This also seems to potentially support the idea that there is always “choice” and perhaps getting the x values to one side first works well in one problem, but in another it may serve better to move the constant values first. So much to admire in this tiny snippet! Thank you for sharing!