I attended NCTM last week, the annual conference of math teachers here in the United States, and my experience was mixed. Nearly all of my mixed vibes related to some combination of my own introversion, the many small rooms filled with lots and lots of people, the specter of COVID leaping out to say “boo!” every so often, etc.
But I also had a feeling—new for me—that teaching needs to become a lot simpler. I don’t think it will ever become easy, but it needs to become simpler, and this is not aligned with the incentives for people who speak at conferences.
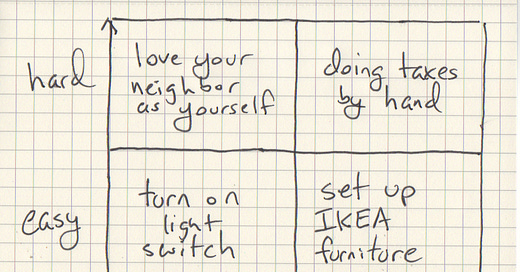
Where is “teaching” in this quadrant? These are subjective judgments to some degree, but I’m going to stipulate that teaching will always be hard. It sits at the nexus of too many loud, competing interests ever to be easy. Plus it involves kids.
Is teaching complex or simple, though? Does it consist of lots of interlocking parts that all demand nearly equal attention? Or can we summarize that work broadly and succinctly?
Conference speakers have every incentive to specialize and differentiate themselves from other conference speakers. They have every incentive to say, “The work of teaching is unknowably complex, but I can help you master that complexity with my special protocol or sixteen step process or framework or flowchart or whatever.”
I’m trying here to separate conference speakers from their incentives—the former being good and noble and buddies of mine and, of course, me myself, while the latter I don’t see serving teachers well in 2022.
We need to name the work of teaching as simply as possible, especially because that work is hard.
If professional learning is a large ocean, teachers would benefit from a single very large anchor to moor them as they drift from learning experience to experience, helping them wonder, “How does this help me with the very hard and very simple job of teaching as I understand it?”
“This session is pointing at the moon,” the teacher might say, “But I understand the moon well and simply enough not to mistake the session for the moon itself.”
The incentives to position the work of teaching as unknowably complex (except through the conference speaker’s frameworks and flowcharts, etc) seems especially true of equity work in education right now where there is a great deal of focus on mastering complex and shifting linguistic conventions and understanding at a very deep level the histories and experiences of the many different intersecting identities in a given classroom, all of which is exceptionally complex and exceptionally hard work. What would it look like to simplify the work of equitable teaching, while still allowing that it is exceptionally hard1?
The most enduring, motivating commandments (like “love your neighbor as yourself”) and both simple and hard. They are memorable and never fully completed, though you can often feel yourself making exciting progress throughout your lifetime in their direction. They help you organize, evaluate, and put to work all kinds of life experiences, especially learning experiences.
This is true of good math instruction, as well, which recognizes that (for example) middle school math is not composed of hundreds of small skills—complex and easy—but rather a small handful of very large ideas that many adults, even those with math degrees, are still working to understand. Simple and hard.
What is the work of teaching, as simply as you can express it?
I offer that the work of teaching, as I understand it, is simply to invite, celebrate, and develop student thinking. Give me another few years and I might be able to simplify that further.
I know that this work will be impossible for me to master in my lifetime, but that definition motivates me daily, and its simplicity helps me learn at conferences like NCTM.
“How is this session helping me figure out and value what a student already knows about math? How is this session helping me understand how to help the student develop their thinking in exciting and important new ways?”
What is the simplest way that you can express the work of teaching?
I think this is an important exercise for any teacher, but especially for my conference speaker colleagues.
What Else?
Related: proposals are due for NCTM 2023 in Washington, DC, tomorrow.
Here’s a gorgeous rendering in Desmos of one of my favorite mathematical illusions. (Tim Ricchuiti.)
Crystal Watson is doing exciting work in math education and has given all of it a new home on the web.
Karina Cousins posted one of my favorite “low floor, high ceiling” tasks, happily bringing back to mind both Malcolm Swan (RIP) and Play With Your Math.
I’ll put my #NCTMLA22 talk online at some point and we can talk about whether or not I’m a part of my own problem here, but until then here are a couple of people’s tweets from it.
I thought Pamela Seda and Kyndall Brown did a great job of this in their NCTM session FWIW. They formulated equity work in their session as something like “caring about what students already know”—not easy but simple!—and offered us strategies and curriculum for doing exactly that.



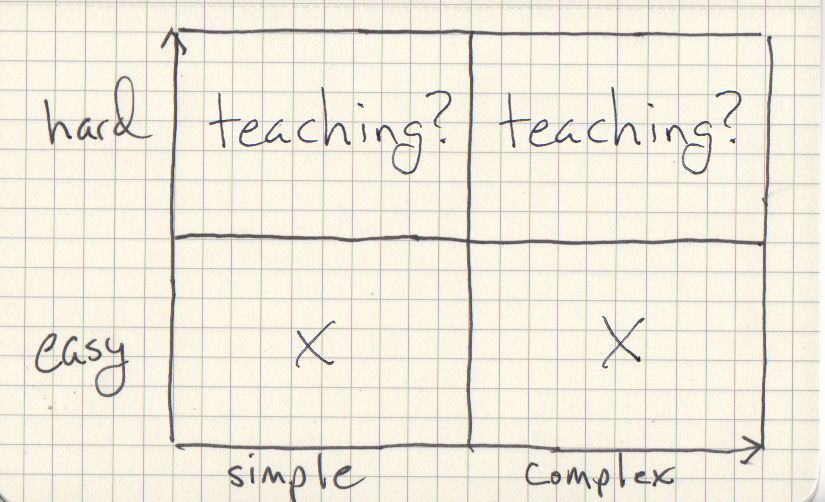

I sometimes think about three possible levels of analysis:
1. The universal level, which I think corresponds to your idea of simplicity: e.g., "Care deeply for your students, and seek to understand their lives." Ideas at this level apply to all teachers everywhere.
2. The level of the society or the community: e.g., "Black students in the U.S. have a shared experience of..." or "First-generation college students have often been told..." Ideas in this level may apply across cities, states, or even countries, but we can also imagine teaching environments where they wouldn't be super-relevant. (E.g., the sociology of U.S. racism is less relevant if you teach in China; the hallmarks of first-gen U.S. college students are less relevant if you teach 2nd grade in Finland.)
3. The level of individual classrooms and students: e.g., "My student Dan was telling me he struggles to find a quiet place to do homework because..." Ideas at this level apply to nobody but me (and maybe a couple of my co-teachers).
It seems like conferences and PD often aim for the middle level. Which makes sense. The universal level can devolve into platitudes; the individual level can devolve into isolated experiences; the societal level aims at things we all share in common, and can thus (maybe!) talk about fruitfully.
The trouble is that the societal level is, as you're pointing out, the most complex and flow-chart-y. "Because of [complex historical pattern], we find [complex sociological pattern], which means that [statistical generality] unless [exception created by different historical pattern]..." That's how I hear your concern about overly intricate PD. This societal level tends to call for a lot of specialized historical and sociological vocabulary.
I'd speculate that the best PD touches all three levels. "Here's a universal value we share. Here's a story of how I struggled to live out that value with a particular student or class. And here's a takeaway about the ways we all (in this society) can reach for that value."
I think Mandy's suggestions (e.g., "What if we thought about teaching math like rough draft and revising?") can work in this way. The speaker articulates a universal reason this might be a fruitful metaphor; teachers share individual experiences in light of that metaphor; and by this process, we all build a shared (societal) understanding of how the metaphor might (or might not) help guide us.
People learn math when they think and interact. The teachers role is to provoke, nurture, nudge thinking and manage (minimally) peer interactions.