Teachers Learning to Become More Interested (and More Interesting)

Trying out a new professional learning experience.

Okay here’s basically my whole thing on a napkin:

A durable finding dating back zillions (sixty) years and replicated in different forms in different studies is that a student’s ability to learn new stuff depends on the stuff they know now. It winds up being an area of rare agreement among educational partisans who otherwise disagree about most things.

One of the biggest challenges here is convincing teachers who are very aware of the math they know that the math their students know is more interesting and more important.

At a session last week in Santa Cruz County, CA, I tried to develop that interest in a systematic way.

1. We split into groups.

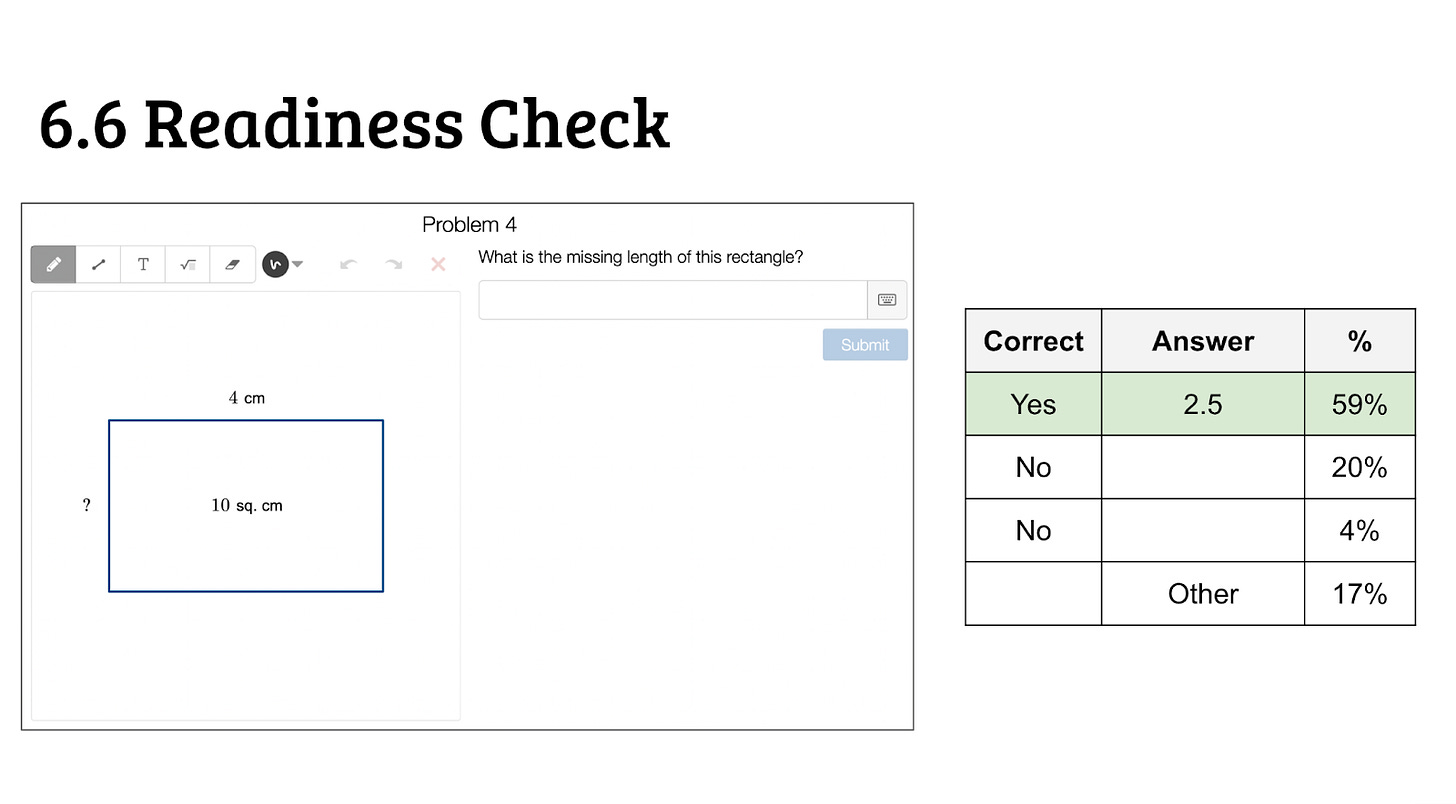
2. We looked at pre-assessment questions for an upcoming unit.

3. We predicted the most common answers to several questions among a national sample of Desmos Math students—awarding ourselves zero points for knowing the correct answer and one point for predicting each of the most common incorrect answers.

4. We revealed the answers and tallied the scores.

The energy was strong and the conversation was tightly focused on student thinking and all the interesting detours students take en route to a correct answer. One teacher would suggest a possible wrong answer that another teacher hadn’t considered and, in explaining the origin of that wrong answer, the first teacher essentially had to make a case that the student was doing something sensible. 

When I revealed that 4% of students incorrectly answered “1 cm” to the question above, a teacher first said, “What??” followed almost immediately by “Ohhh .…” as he realized that students had correctly solved for the perimeter of 10 rather than an area.

I don’t want to make too much of that moment but we should make something out of it. In a moment, just a blink, a teacher went from imagining students and their thinking to be alien and nonsensical to imagining them sensible and clever even when they’re wrong. 

A common feature of engaging teachers is that they’re engaged. Engaged with their discipline, yes, but also engaged with you, the student. Engaged by you and your thinking. It’s easy to imagine those teachers are born, rather than made. But I’m wondering lately whether exercises like the one above, repeated over time, can help make more engaging and more effective teachers.