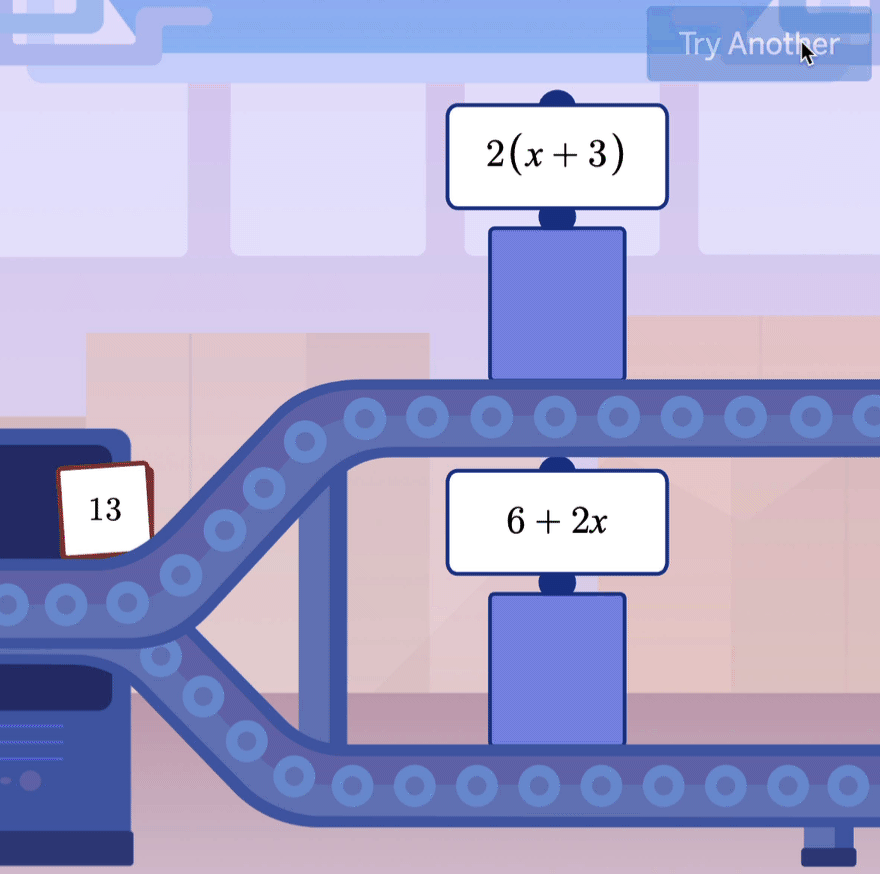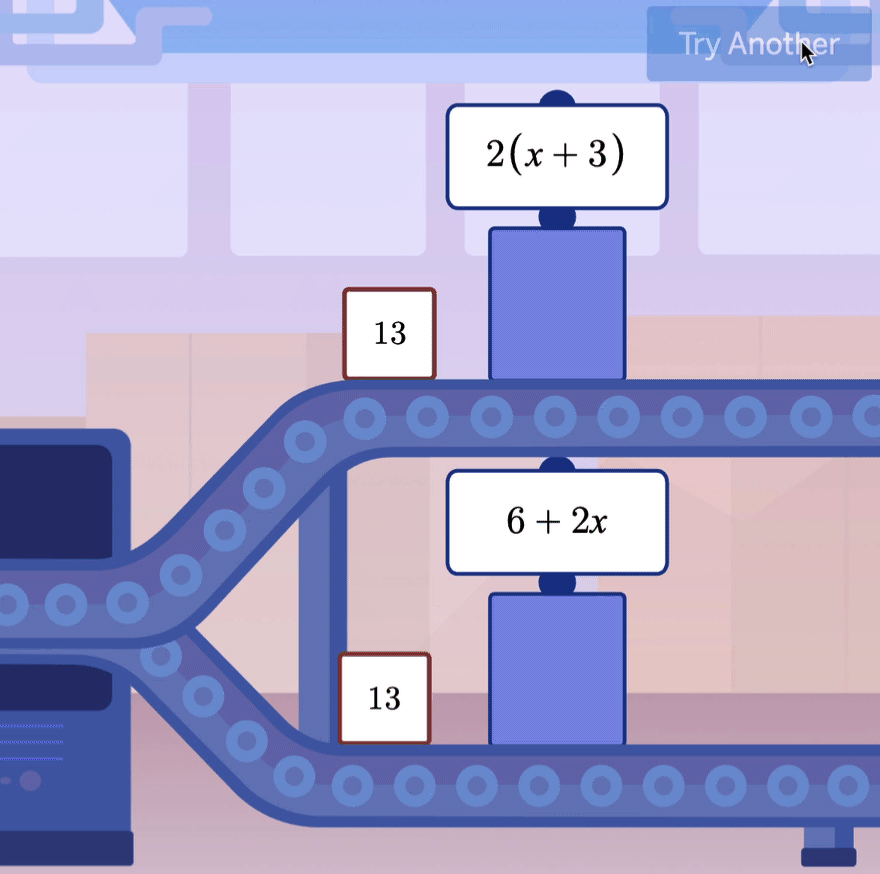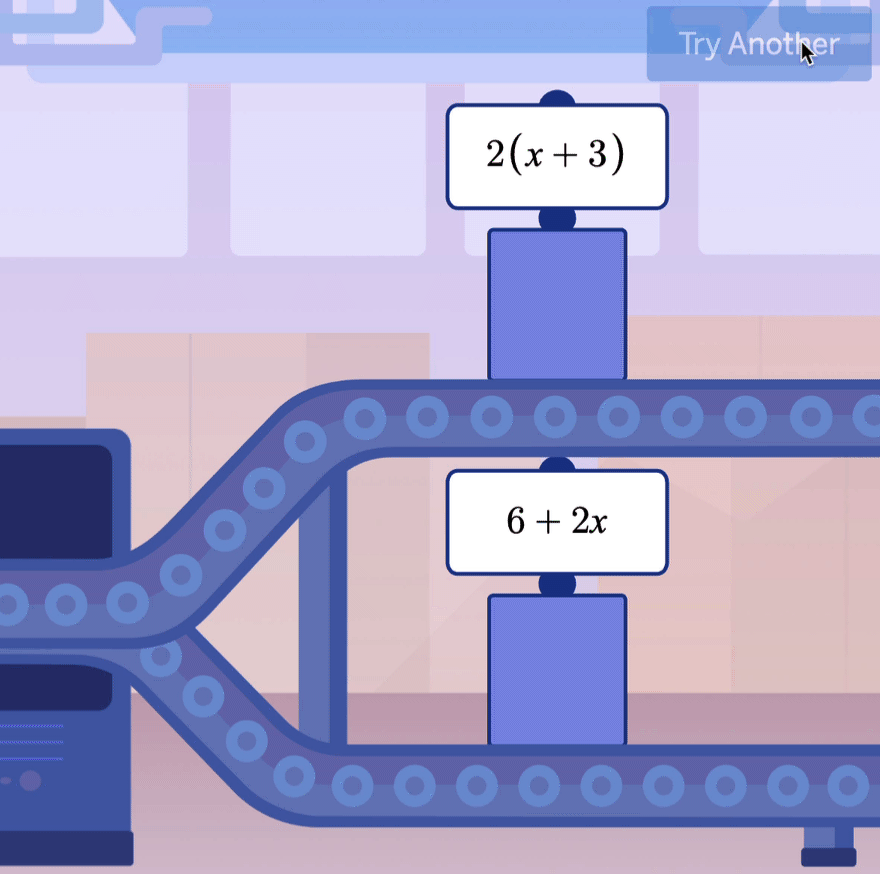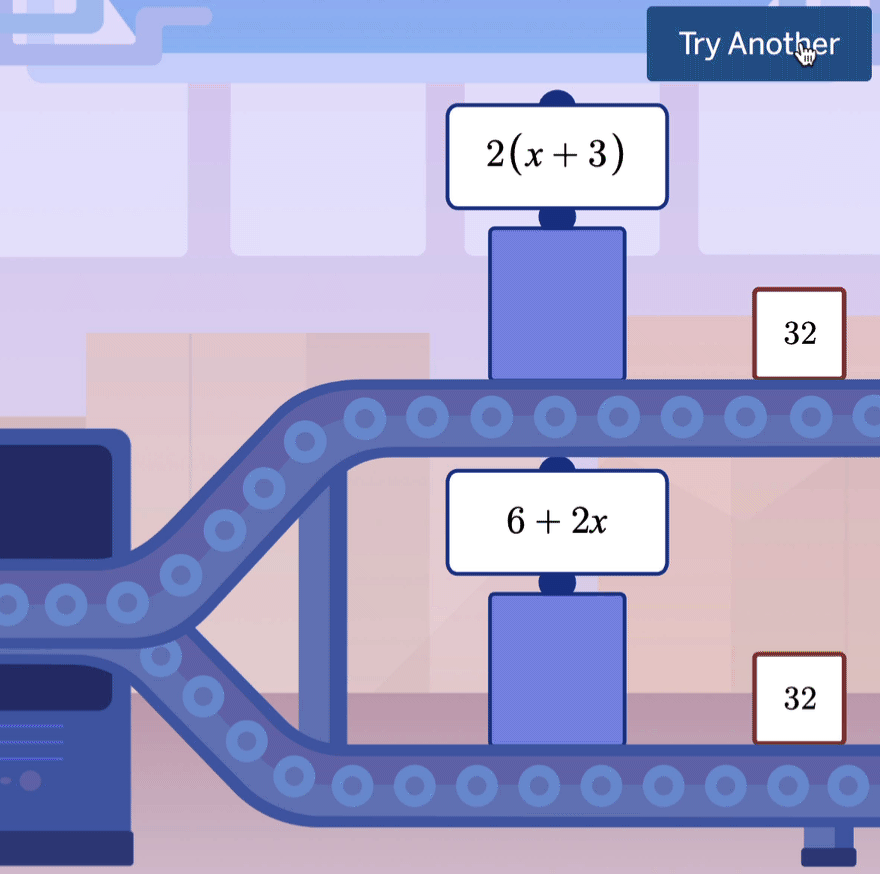
In a recent post, I noticed it was pretty easy to get Khanmigo, Khan Academy’s AI chatbot tutor, to cough up the answer to a question if you just whined at it hard enough.
“IDK” I told Khanmigo in response to its every gentle, Socratic nudge, and eventually Khanmigo said, effectively, “Okay here is the answer. Does it make sense?”
Human tutors aren’t so easily manipulated and if you believe AI chatbot tutors should someday approximate human tutors, these are the problems you have signed up to solve.
As is frequently the case, some Khanmigo product changes followed my post critiquing Khanmigo. Now, when I spam Khanmigo with IDKs, Khanmigo effectively stonewalls, saying, “Okay look, here are some resources to watch or read. Quit wasting my GPT tokens with your nonsense.”
This is an interesting development! The website JoySchooler is another platform that refuses my manipulation, saying, “Let’s take a break,” and then disabling the chat box.
My opinion is that these are both interesting developments and worth sharing with you, but they both still look a lot like hell. It still seems like deeply alienating work, trying to build a skilled human teacher from a sack of LLM prompts, one with low odds of success. With every new step towards your destination, you realize it’s two steps farther than you thought. Every new line of your prompt risks contradicting a previous one. You write a new line to meet a new student need and accidentally unmeet an older one.
And let’s say you manage to create a chatbot that says exactly what a skilled human tutor would say at every turn in a tutoring interaction. Will we then see skilled human tutor results from the chatbot or will we find that the real liability here wasn’t that the chatbots were saying the wrong things but that kids don’t care what chatbots have to say? These are the questions you have signed up to answer.
Too many to share from last week’s post on teaching the long cut, but I liked Kristi Peterson’s description of “skipping the math” a lot:
I love using the "long cut" for graphing linear equations. When working with the Slope-intercept Form, most resources I've used go straight for the short cut of plotting the y-intercept and using the slope to plot the points of the line, but this is usually meaningless to the students. Instead I require that they use a table, then identify the slope and intercepts. Usually after about 20 linear equations, they see it for themselves. Then they think they can trick me by "skipping the math" and just plotting one point and using the slope -- jokes on them :)
Also Bryan Kerr on why so many software developers find ideas like a “Personalized Netflix for Education” so seductive:
I think Netflix-i-fying content may work well for those with high intrinsic motivation. I'd love it if I could get customized videos to help me vibe code something that helps me solve an important problem. But edtech companies may be putting the cart before the horse as their designs seem to take for granted that students already see the value in what the software delivers to their screens. Maybe the developers just assume kids are as highly motivated as they were back when they devoured YouTube videos learning to code.
¶ David Wiley is a smart guy but he’s trying to do the wrong thing the right way by teaching an LLM about pedagogical content knowledge. How … can I put this more simply? Kids do not seem like they want to talk to LLM chatbots about academic content, no matter how well they are trained. The oracle might contain all knowledge and know the answer to every question, but none of that matters if she is surrounded by dragons and an acid moat. The medium inhibits the message.
¶ More from Khan Academy. First, Sal Khan has an interview with CNBC where he says:
The tools are exciting and we’re investing a lot in this front but in most cases it’s about how you integrate it with the classroom, how you help the teacher hold the students accountable, engage them, and then the students will be off to the races.
I think that’s exactly right and I am very curious how Khan Academy intends to “help the teacher.”
¶ Recent predictions from some edtech luminaries. Bill Gates was on Jimmy Fallon’s show and said:
The era that we’re just starting is that intelligence is rare, you know, a great doctor, a great teacher, and with AI over the next decade, that will become free, commonplace. Great medical advice, great tutoring.
I just want to note the sleight-of-hand that turns a “great doctor” into “great medical advice” and a “great teacher” into “great tutoring.” Which people get which of those resources is going to be a matter of intense debate over the next decade and we must not pretend they are the same thing.
Another interesting prediction. Sal Khan recently told the National Governors Association:
I think the best scenario is that in 2034 if you are a teacher, you can spend 90% of your time on student-facing tasks.
Wait—that’s what he said about 2024!
Looking ahead to 2024, I see generative AI tools cutting 90% of teachers’ admin tasks, creating more time for student interaction.
AI was supposed to give teachers 90% of their time back at the end of 2024, Sal! Now they have to wait ten more years? What is going on?
There are lots of contexts where missing your forecasts by 10x would immediately discredit a person, but edtech is apparently not one of them. In edtech, you will never get asked, “So what happened there? What’d you miss? Did you misunderstand the ed or the tech or both?” In edtech, it seems we’re all just having a bit of fun.
¶ Our edtech luminaries are softening their predictions for generative AI. The biggest generative AI IPO underperformed expectations. Microsoft is canceling data center leases. Salesforce’s big AI play isn’t delivering on revenue expectations. There is increasing evidence inside and outside of education that generative AI is not anywhere close to delivering on its promises. I still think this technology is neat but the sooner we grip the possibility that it isn’t much more than that, the sooner we can get back to work.
¶ Tressie McMillan Cottom names generative AI a “mid technology” in the New York Times:
That tech fantasy is running on fumes. We all know it’s not going to work. But the fantasy compels risk-averse universities and excites financial speculators because it promises the power to control what learning does without paying the cost for how real learning happens.
¶ I’m a huge fan of the CourseKata team and their joyful approach to data science and statistics. They’re offering a fellowship for high school teachers that includes free PD and curriculum. Priority is given to early applicants, so I encourage you to check out the opportunity.